Каркасный арочный ангар
Комплектация:
-винтовые сваи;
-арки, прогоны, связи;
-торцы, ворота;
-кровельное покрытие профлистом;
-болтовые соединения.
Ширина пролелета: 10 - 30 метров.
Длина ангара - до 96 метров.
Производство Каркасных Ангаров и Зданий
Производство Бытовок и Вагончиков
Производство Винтовых Свай, Фундаментные работы
Разработка Проектов
Изготовление Металлоконструкций по чертежам Заказчика
тел.:8 (922) 878-30-95
Принимаем звонки с 06:00 до 20:00 МСК
e-mail: info@k-angar.ru
Работаем по РФ и СНГ
Расчет площади поверхности арочного ангара
При возведении ангаров из металлических конструкций нередко возникает вопрос о том, как точно определить площадь кровельного материала для закупки. Если расчёт площади двускатной крыши не представляет особых проблем, то с вычислением площади арочной крыши многие сталкиваются с трудностями. Ниже мы рассмотрим, как правильно определить площадь поверхности арочного ангара.
На самом деле, здесь нет ничего сложного. Нужно лишь вспомнить школьный курс геометрии. Нам нужно вычислить площадь поверхности половины цилиндра.
Как мы помним со школы, площадь боковой поверхности цилиндра рассчитывается по формуле: S=2πRh, площадь основания цилиндра: S=πR2, а общая площадь поверхности цилиндра: S=2πR(R+h), где
π – 3,14,
R – радиус цилиндра
h – высота цилиндра
Как рассчитать площать арочного ангара
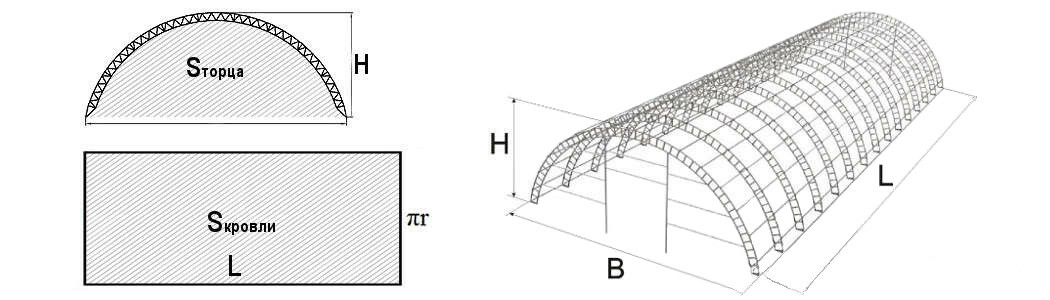
Нам необходимо учитывать, что площадь поверхности арочного ангара равна половине площади цилиндра, то есть S=πR(R+h), при условии, что ангар имеет правильную арочную форму, где высота по коньку равна половине ширины ангара, это и будет радиус.
Но если высота ангара не равна половине ширины, то есть ангар имеет вытянутую форму, например при ширине ангара в 20 метров и высоте по коньку 8 метров, то необходимо в формулу внести некоторые корректировки. Здесь математическая формула в чистом виде нам уже не поможет, так как придется иметь дело с интегралами. А нам оно зачем? Такая точность расчетов ни к чему.
Если мы возьмем за радиус половину ширины ангара, то у нас расчетная площадь получится больше фактической, что приведет к закупкам лишнего кровельного материала. Если за радиус принять высоту по коньку, то кровельного материала может не хватить. Практика показала, что в данном случае за радиус стоит принимать среднее арифметическое значение. То есть взять половину ширины ангара, в нашем случае 20/2=10м. сложить с высотой 8м. и поделить на 2. В итоге за радиус необходимо принять значение (10+8)/2=9м.
Давайте попробуем рассчитать площадь стандартного арочного ангара 1000 м2 – 20х50 метров с высотой по коньку 8 метров.
S=3,14 х 9 (9+50) = 1667,34 ≈ 1668 м2.
Расчет кровельного материала для покрытия арочного ангара
Рассчитаем, сколько кровельного материала нужно для ангара. Предположим, что у нас есть только одни торцевые ворота размером 4 на 6 метров. Если ворота будут покрыты тем же материалом, что и весь ангар, то их площадь не вычитаем из общей площади поверхности. Если же ворота сделаны из другого материала, их площадь можно вычесть (1668 - 24 = 1644 м²).
Возьмем стандартный профилированный лист. Его размеры: рабочая ширина 1150 мм, длина 6000 мм. Площадь одного листа составляет 6,9 м². Чтобы определить, сколько листов нам нужно, разделим общую площадь поверхности ангара на площадь одного листа: 1644 м² / 6,9 м² = 238,26. Округляем в большую сторону и получаем 239 листов. Это условный расчет. Если вы планируете делать нахлест в две волны, количество листов увеличится. В расчетах учитывайте только рабочую поверхность листа, как по ширине, так и по длине. Помните, что при покрытии торцов ангара часть листов придется обрезать по радиусу арки.
Простой калькулятор расчета площади кровли арочного ангара
Данный расчет произведен по условно допустимой формуле описанной выше.
Если Вам необходимо произвести расчет стоимости для строительства ангара по указанным габаритам, то оставьте заявку на расчет, мы свяжемся с вами и предоставим подробную смету по материалам и стоимости услуг.
Что мы можем Вам предложить
ООО «Каркасные Конструкции» осуществляет строительство каркасных арочных ангаров под ключ, а также реализует каркасы сооружений для самостоятельного монтажа. Наши производственные мощности — это несколько цехов с современными высокоточными станками по обработке металла: это лазерная резка листового металла, лазерная резка профилированной и круглой трубы, гибка металла и др.
Производим и реализуем металооконструкции, арки, фермы
Поставляем каркасы ангаров для самостоятельного монтажа
Строим каркасные арочные ангары "Под ключ" по всей России
Доверьте работу профессионалам. Мы сами посчитаем объем необходимого для строительства материала. Возьмем поставки и логистику на себя. Сдадим объект точно в срок с гарантией на все производимые работы в течение 60 месяцев.
Наиболее востребованные ангары
Уточнить цену
Арочный ангар с вертикальной стеной
Комплектация:
-винтовые сваи;
-арки, прогоны, связи;
-торцы, ворота;
-кровельное покрытие профлистом;
-болтовые соединения.
Ширина пролелета: 6 - 24 метра. Длина ангара - до 72 метров.
Уточнить цену
Каркасный прамостенный ангар с двускатной крышей
Комплектация:
-винтовые сваи;
-фермы, прогоны, связи;
-торцы, ворота;
-кровельное покрытие профлистом;
-болтовые соединения.
Ширина пролелета: до 30 метров. Длина ангара не ограничена.
Уточнить цену
Мы уже построили
Два каркасных арочных ангра Тип "А" 20х50
Арочное Зернохранилище 20х50
Четыре каркасных ангара Тип "С" 15х30
Арочное Зернохранилище Тип "В" 24х61. Московская область.
Два каркасных арочных Зернохранилища Тип "В" 20х50
Крытый ток с вертикальной стеной Тип "В" 21х51
И еще более 200 объектов по всей стране. Оставьте заявку, и мы покажем Вам построенные объекты именно в Вашем регионе, чтобы Вы могли пообщаться с заказчиком и убедиться в качестве нашей работы.
Запросить КП
Почему заказывают ангары у нас
build
Сборно-разборная конструкция
В отличие от других металлических конструкций, сборно-разборный ангар обладает высокой степенью мобильности и может быть легко собран в любом новом месте. Если ваша компания меняет направление деятельности или происходят изменения в характере работы, то перепрофилировать или переместить ангар не составит труда. Также его можно продать как отдельное сооружение без привязки к земле.
access_time
Сжатые сроки строительства
В сжатые сроки мы создаём металлические конструкции для ангаров. Они изготавливаются на нашем производстве под конкретный заказ, а затем собираются и устанавливаются на строительной площадке. Благодаря точной подгонке элементов друг к другу, мы гарантируем отсутствие технических дефектов. Лёгкие конструкции для ангаров позволяют обойтись без использования специальной техники для их транспортировки и монтажа. Для работы достаточно группы рабочих от 5 человек и более, в зависимости от масштаба проекта.
assignment
Не требует разрешения
Сборно-разборная конструкция на болтах — это не капитальное строение, а временное сооружение. Для её возведения не нужны разрешительные документы. Благодаря прочному металлическому каркасу конструкция надежна и устойчива: выдерживает землетрясения до 6 баллов, а также ветровые и снеговые нагрузки до 480 кгс/м².
ac_unit
Работаем в любых климатических условиях, вне зависимости от сезона и времени года
Выбор места для строительства ангара практически неограничен. Ландшафт на участке не изменится. Не нужно проводить сложные земляные работы. При больших нагрузках на каркас ангара фундамент делают свайно-винтовым. Если качество грунта позволяет, можно установить столбчатый фундамент. На слабых грунтах используют ленточный фундамент. Что лучше в каждом случае, подскажет наш опытный специалист.
Остались вопросы?
Для получения подробной консультации позвоните
нашим менеджерам по телефону 8 (922) 878-30-95
или закажите обратный звонок.
Мы Вам перезвоним в течении 7 минут.
О компании
- ООО "Каркасные Конструкции", г. Оренбург, ул. Цвиллинга, д.46, 309, 460006
- +7 (922) 878-30-95
- info@k-angar.ru
- 5611065547, Проектирование, производство и строительство Каркасных Ангаров и Зданий и сооружений